LeetCode::LinkedList(Part1)-Without Modifying the List
Introduction
This post will cover some of the programming challenges on singly linked list from LeetCode. In particular, I will only focus on problems that can be solved without modifying the list itself. The more challenging and (argubly) interesting problems will be discussed in the second and third part of the series.
141. Linked List Cycle
Description & Example
Given a linked list, determine if it has a cycle in it.
Solution 1 (Tortoise and Hare)
bool hasCycle(struct ListNode *head) {
struct ListNode* slow, *fast;
slow = head, fast = head;
while(fast && fast->next){
slow = slow->next;
fast = fast->next->next;
if (slow == fast)
return true;
}
return false;
}This is a well-known solution to a well-studied problem. I will only give a simple explanation of why the fast and slow pointers will eventually meet if there is a cycle.
Suppose a cycle exists, then by the time the tortoise gets in it, the hare will already be somewhere inside. From that point, the hare will be catching up to the tortoise in the cycle. Since the hare is running twice as fast, it is guarantueed to be one step closer each loop, eventually meeting the tortoise.
Solution 2 (Brent’s algorithm)
142. Linked List Cycle II
Description & Example
Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
Solution
From this discussion
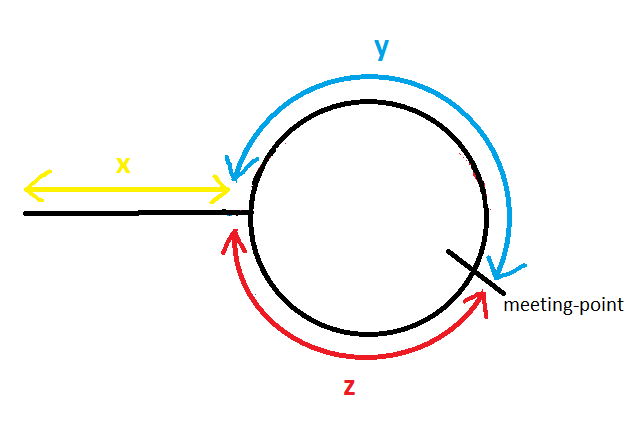
Suppose we have run the tortoise and hare algorithm and they meet at the meeting point as shown in the image. Note that the tortoise is guranteed to be caught up by the hare within one cycle after it enters the cycle. But the hare could have travelled the cycle m times before the tortoise enters the cycle. Then we have:
- Distance run by tortoise: $x + y$
- Distance run by hare: $x + m(y+z) + y$
Since the hare has been running at twice the speed of the tortoise, we have:
\[2(x+y) = x + m(y+z) + y\]Sovling for $x$ gives:
\[x = (m-1)(y+z) + z\]What this tells us is that in another scenario, if we have two pinters, one starting at the head of the list and the other starting at somewhere in the cycle and running at the same speed. Then by the time the first pointer enters the cycle (aka travelled a distance of $x$), the second pointer will have moved forward a distance of $z$ relative to its starting position.
Now it should be clear why the following algorithm works:
- Run the tortoise and hare algorithm. Now both slow and fast pointer are at the meeting point as showin in the image.
- Move the slow pointer to the beginning of the list again. Set the fast pointer to be running at the same speed as the slow pointer.
- Move both pointer in parallel until they meet. The new meeting point would be at the start of the cycle.
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode* slow, *fast;
slow = head, fast = head;
while(fast && fast->next){
slow = slow->next;
fast = fast->next->next;
if (slow == fast){
slow = head;
while(slow != fast){
slow = slow->next;
fast = fast->next;
}
return slow;
}
}
return NULL;
}160. Intersection of Two Linked Lists
Description & Example
Write a program to find the node at which the intersection of two singly linked lists begins.
Notes:
- If the two linked lists have no intersection at all, return null.
- You may assume there are no cycles anywhere in the entire linked structure.
Solution
There are surprisingly many solutions to this problem, but here I will only present one that’s easy to understand. The idea is simple:
- Traverse the lists and compute their lengths, called it
lenAandlenB - Move the head of the longer list
abs(lenA-lenB)nodes ahead, so that now headA and headB are sitting at the same distance from tail - Traverse headA and headB in parallel and compare the address of each node along the way. If they are equal, it is the intersection point
def getIntersectionNode(headA, headB):
curA,curB = headA,headB
lenA,lenB = 0,0
while curA is not None:
lenA += 1
curA = curA.next
while curB is not None:
lenB += 1
curB = curB.next
curA,curB = headA,headB
if lenA > lenB:
for i in range(lenA-lenB):
curA = curA.next
elif lenB > lenA:
for i in range(lenB-lenA):
curB = curB.next
while curA and id(curA) != id(curB):
curA = curA.next
curB = curB.next
return curA876. Middle of the Linked List
Description & Example
Return the middle node of a linked list. If there are two middle nodes, return the second one.
Solution
struct ListNode* middleNode(struct ListNode* head) {
if (head == NULL || head->next == NULL)
return head;
struct ListNode* slow, *fast;
slow = head, fast = head;
while(fast && fast->next){
slow = slow->next;
fast = fast->next->next;
}
return slow;